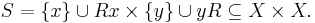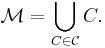Szpilrajn extension theorem
In mathematics, the Szpilrajn extension theorem, due to Edward Szpilrajn (1930) (later called Edward Marczewski), is one of many examples of the use of the axiom of choice (in the form of Zorn's lemma) to find a maximal of a set with certain given properties.
The theorem states that, given a binary relation R that is irreflexive and transitive it is always possible to find an extension of the relation (i.e. a relation T that strictly includes R) which is asymmetric, negatively transitive and connected.
First of all, we need some definitions to be clear upon the terminology we will use speaking about relations with particular properties.
Contents |
Definition (negative transitivity)
Given a binary relation 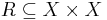 on a generic set
on a generic set  , we say that
, we say that  is negatively transitive if
is negatively transitive if
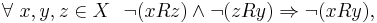
- where by
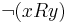 we mean
we mean 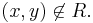
Note that negative transitivity can also be rewritten as :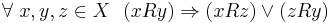 , simply using the fact that
, simply using the fact that 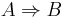 can be rewritten as
can be rewritten as 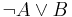
Definition (connection)
Given a binary relation 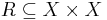 on a generic set
on a generic set  , we say that R is connected (weakly) if :
, we say that R is connected (weakly) if :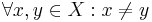 either
either 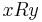 or
or 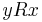 .
.
- We say that R is strictly connected or complete if
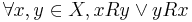 .
.
Properties
This properties on binary relations can be easily checked by definition:
- R is irreflexive and transitive
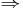 R is asymmetric.
R is asymmetric. - R is asymmetric, transitive and connected
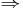 R is negatively transitive.
R is negatively transitive.
To enounce precisely the theorem, we need yet a couple of definitions and a useful, simple lemma.
Definition (strict orders)
- We say that a binary relation R is a strict partial order if it is irreflexive and transitive.
- We say that a binary relation R is a strict order if it is asymmetric, negatively transitive and complete.
Lemma
Let R be a strict partial order on X. Then there exists another binary relation T on X which is still a strict partial order and extends R, hence:
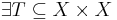 such that
such that 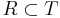 and T is another strict partial order on X.
and T is another strict partial order on X.
This lemma can be easily proved, by taking 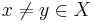 such that
such that 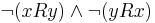 , which exists since the relation is not connected.
, which exists since the relation is not connected.
- Naming:
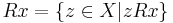
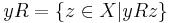
we can define another relation:
Finally, set 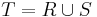 which is trivially an extension of R and another strict partial order on X.
which is trivially an extension of R and another strict partial order on X.
Theorem (Szpilrajn's extension theorem)
Let R be a strict partial order on a set X. Then there exists a relation T that extends R and is a strict order on X.
Proof
- Let
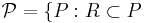 , P is a strict partial order on X
, P is a strict partial order on X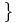 .
.
We want to show the existence of a maximal element in 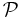 with respect to set inclusion.
with respect to set inclusion.
To do this, we will use Zorn's Lemma. First of all we want to verify the hypothesis of the Lemma, hence that any chain (respect to inclusion) of 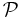 admits an upper bound in
admits an upper bound in 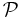 .
.
Let  be a chain in
be a chain in 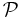 .
.
Define
Clearly 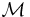 is an upper bound to the chain, but we have to show that
is an upper bound to the chain, but we have to show that 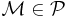 , hence that
, hence that 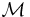 is another strict partial order which extends R.
is another strict partial order which extends R.
Obviously it contains R, as all 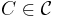 contains R, and it is irreflexive, as
contains R, and it is irreflexive, as 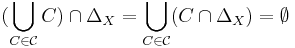 , since any
, since any
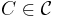 is irreflexive,
is irreflexive,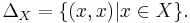
We have to show that 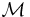 is transitive and here we use the chain properties of
is transitive and here we use the chain properties of  .
.
Let 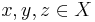 such that
such that 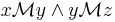 iff
iff 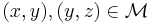 .
.
As 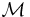 is defined as a union of sets, there exists
is defined as a union of sets, there exists
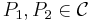 such that
such that 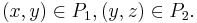 .
.
But  is a chain with respect to inclusion, hence it holds that
is a chain with respect to inclusion, hence it holds that 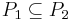 or viceversa, so that the two couples of elements of X both belong to the same set in the union, and that set is a transitive relation; then also
or viceversa, so that the two couples of elements of X both belong to the same set in the union, and that set is a transitive relation; then also 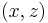 is in that set, hence in
is in that set, hence in 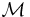 .
.
Applying Zorn's Lemma, we deduce that 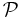 admits an upper bound with respect to set inclusion; let's call T that bound.
admits an upper bound with respect to set inclusion; let's call T that bound.
T has to be a complete relation, as if it was not, we could construct (exactly as in the preceding Lemma) another binary relation which strictly extends (strictly includes) T and is a strict partial order, so yet another element of 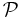 , contradicting that T is a maximal of
, contradicting that T is a maximal of 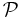 .
.
So T is an irreflexive, transitive and complete binary relation on X. But as we observed above, irreflexivity and transitivity give asymmetry that, with transitivity and completeness, give negative transitivity.
Hence T is a strict order on X that extends the partial order R.
References
- Szpilrajn, E. (1930), "Sur l'extension de l'ordre partiel", Fundamenta Mathematicae 16: 386–389, ISSN 0016-2736, http://matwbn.icm.edu.pl/tresc.php?wyd=1&tom=16